Simple Linear Regression : Gradient Descent Method
⛄ Gradient Descent Method(경사하강법)
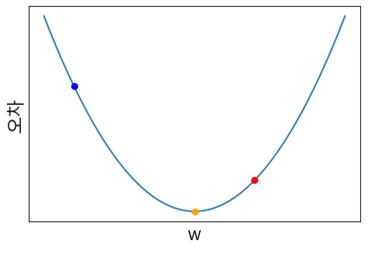
비용함수를 최소화하는 와 를 구하는 최적화 알고리즘을 옵티마이저(Optimizer)라고 하는데, 경사하강법(Gradient Descent)은 가장 기본적인 옵티마이저이다. 이때, 경사하강법의 기본 개념은 함수의 기울기를 구하고 경사의 절댓값이 낮은 쪽으로 계속 이동시켜 극값에 이를 때까지 반복시키는 것이다.
(예를 들어, 위 사진의 경우 노란색 점에 도달하고자 함)
그런데, 우리는 보통 함수의 최솟값을 찾고자 할 때 미분계수를 구함으로써 찾는다. 이 방법을 사용하지 않고 경사하강법을 사용하는 이유는 무엇일까?
1. 실제 분석에서, 특히 딥러닝 알고리즘을 활용하는 경우에 보게 되는 함수들은 형태가 굉장히 복잡해서 미분계수와 그 근을 계산하기 어려운 경우가 많다.
2. 미분계수 계산 과정을 컴퓨터로 구현하는 것보다, 경사하강법을 구현하는 것이 훨씬 쉽다.
3. 데이터의 양이 매우 큰 경우 경사하강법과 같은 순차적인 방법이 계산량 측면에서 훨씬 효율적이다.
자, 이제 본격적으로 경사하강법에 대해서 알아보자.

경사하강법은 함수의 기울기(=gradient)를 이용해서 함수가 최솟값 일 때의 값을 찾기 위한 방법이다. 기울기가 양수인 경우는 값이 증가할수록 함수 값도 증가하고, 반대로 음수인 경우에는 값이 증가할수록 함수 값이 감소한다.
이 점을 이용해서 기울기가 양수라면 음의 방향으로 를 옮기면 되고, 기울기가 음수라면 양의 방향으로 를 옮기면 된다.
--> xi+1=xi−이동거리×기울기의 부호
그런데, 이동거리는 어떻게 구해야 할까?
미분 계수(=기울기=gradient)는 극소값에 가까워질수록 값이 작아진다. 따라서, 이동거리에는 미분 계수와 비례하는 값을 이용한다. 그럼 극소값에서 멀 때는 많이 이동하고, 극소값에 가까울 때는 조금씩 이동할 수 있다.
이에 따라 최종적으로 유도되는 공식은 다음과 같다.

이때 = step size, learning rate(hyperparameter)
⛄ Step size, Learning rate ( =)
이제 중요한 것은
